カオスについて２ - daruma3940の日記

daruma3940.hatenablog.com
f:id:daruma3940:20160520223745p:plain
院試も終わったし前回の続きをかくのじぇ
前回2次元調和振動子は摂動を加えられなければトーラスになり、
摂動が弱い場合でも元のトーラスは変形して新しいトーラスができ、摂動が強くなるとトーラスが壊れてカオスが発生するらしいことについて書いたのじぇ。

f:id:daruma3940:20160520223745p:plain
ここでポアンカレマップについて説明するのじぇ。
ポアンカレマップとはトーラスの断面を切り取ったものなのじぇ。
f:id:daruma3940:20170824112349p:plain

2次元調和振動子の場合は変数はx,y,px,pyの4つであるけれど、
ハミルトニアンが一定という条件
${ \displaystyle H_0 = \sum_{i=1,2} (p_i^2+\omega_i^2q_i^2)/2 }$
から変数（例えばpy）を一つ消せ、
y=0の点となった時に点をプロットするということをすれば
変数はx,pxだけになるので2次元平面に点をプロットできるようになるというわけのじぇ。
↓こんな感じ
f:id:daruma3940:20170824114046p:plain
f:id:daruma3940:20160520223745p:plain
ここで非加積分系について考えようじぇ。
${ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }$

f:id:daruma3940:20170824142059p:plain
周期軌道から少しずらしたものがポアンカレマップのどこに来るのかを考えると

${ \displaystyle \delta x(T)=M \delta x(0) }$

となるのじぇ。
このMは安定性行列と呼ばれ、保存系ではdet(M)=1となるのらしいのじぇ（よくわかってない）
これはリウビルの定理と呼ばれるものなのじぇ（リウビルの定理って正準変換のところで出てきたけど...）
${ \displaystyle M = \left( \begin{array}{ccc} a & b \\ c & d \end{array} \right) }$
とすると
${ \displaystyle M \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} a \\ c \end{array} \right) }$
${ \displaystyle M \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} b \\ d \end{array} \right) }$
となり、
f:id:daruma3940:20170824143433p:plain
　　　　　　　　　　　　↓
f:id:daruma3940:20170824143442p:plain

面積S=ab-bc=det(M)=1
になるのでdet(M)は面積が何倍されたかを表すのじぇ。
ここで行列Mの固有値について考えると
${ \displaystyle det(M)=\lambda_1 * \lambda_2=1 \\ \lambda_1 = 1/\lambda_2 }$

ここでもし固有値が実数で重解ではない場合、どちらか片方は固有値が1より大きく片方が固有値が1より小さくなるのじぇ
ということは片方は写像を繰り返すたびに指数関数的な拡大をし、
片方は写像を繰り返すたびに指数関数的に小さくなっていくのじぇ。
f:id:daruma3940:20170824163326p:plain
f:id:daruma3940:20170824163339p:plain
安定方向の直線上にない、つまり安定成分と不安定成分を持っているものは不安定性の指数関数的増加に引っ張られて不安定方向に流されていくのじぇ
f:id:daruma3940:20170824164353p:plain
もし固有値が複素数の場合、
λ1はλ２の複素共役かつλ1*λ２=|λ1|^2=1なので
${ \displaystyle \lambda_1 =exp(i \theta) \\ \lambda_2 =exp(-i \theta) }$
になりこのような行列Mは
${ \displaystyle M = \left( \begin{array}{ccc} cosθ & sinθ \\ -sinθ & cosθ \end{array} \right) }$
であり、これは回転行列なのじぇ。
これは指数関数的に拡大しないため安定なのじぇ。
f:id:daruma3940:20170824191827p:plain
もし重解を持った場合、
λ1=λ2=1であり、このような固有値を持つ行列は
${ \displaystyle M = \left( \begin{array}{ccc} 1 & a \\ 0 & 1 \end{array} \right) }$
であり
${ \displaystyle M \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) }$
${ \displaystyle M \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} a \\ 1 \end{array} \right) }$

となるのじぇ。
図に書くとこんな感じ。
f:id:daruma3940:20170824191749p:plain

これも指数関数的に大きくなっていくわけではないので安定（中立安定）なのじぇ（この図あんまり理解できていない）
f:id:daruma3940:20170824191805p:plain

もし上のハミルトニアンでk=0のときこれは加積分系であり、周期軌道から少し初期値をずらしても別の周期軌道に乗るだけなのでこれは指数関数的に大きくなっていかず、中立安定的なのじぇ
しかしkが大きくなっていくとトーラスが壊れ、もしそれが複素数のほうへ壊れたのなら、安定固定点が発生し、実数のほうへ壊れたのなら不安定固定点が発生するのじぇ

このようすをkicked rotatormodelで描いてみるとこんな感じになったのじぇ
kicked rotatormodelとは
周期的に撃力を受ける回転子のことで....って書くのはめんどくさいので
http://a-phys.eng.osaka-cu.ac.jp/suri-g/phys8.html
このページを見てくれだじぇ
f:id:daruma3940:20170824160407p:plain

これがK（キックの強さ）=0の時
キックのじゃまを受けないのでひたすらθは大きくなっていくのじぇ
f:id:daruma3940:20170824160307p:plain
こんな感じ　まさしく中立安定
K=0.01のとき
f:id:daruma3940:20170824160435p:plain
K=1.2の時
f:id:daruma3940:20170824160514p:plain
島みたいなのが現れているのじぇ。これが複素数の方向に壊れたやつなのじぇ。
島と島の間には実数の方向に壊れたやつが存在しているけどカオス的になってしまっているので構造はみてとれないのじぇ
ちなみにこの島を拡大すると島の中にも島が存在するのじぇ。これはいわゆるフラクタル的構造なのじぇ
f:id:daruma3940:20170824160921p:plain
さらにキックを強くするとこんな感じ
f:id:daruma3940:20170824160713p:plain

これらの図は範囲が違ったりするので注意なのじぇ
Kが大きくなると完全にカオス的になるのはすべて実数方向にずれるから？？
安定固定点と不安定固定点が交互に出てくるのはなぜ？？？
さっきの
${ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }$

についてもやってみたけどそんなにきれいなのは見られなかったのじぇ
でもまあ一応張っておくか
f:id:daruma3940:20170824183931p:plain
f:id:daruma3940:20170824172501p:plain
f:id:daruma3940:20170824195423p:plain
f:id:daruma3940:20170824223802p:plain
f:id:daruma3940:20170824223818p:plain
f:id:daruma3940:20170825113033p:plain
f:id:daruma3940:20170824223831p:plain
f:id:daruma3940:20170826195420p:plain
f:id:daruma3940:20170826184006p:plain

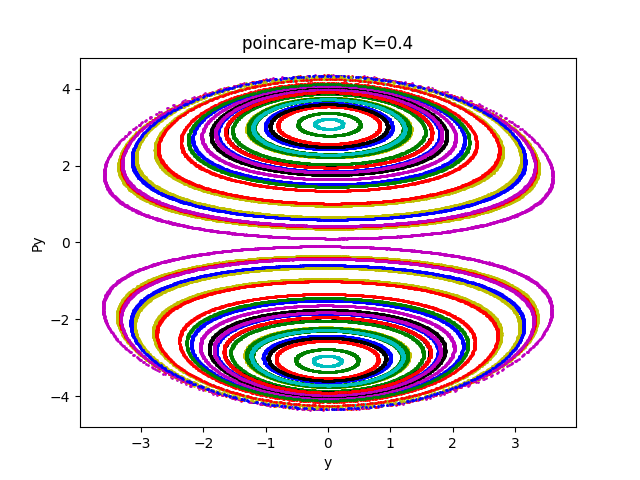
なんかうまくいかないなーー
なんでだろうだじぇ？

う～～んう～～ん......
f:id:daruma3940:20160520223745p:plain
分かったのじぇ
ハミルトニアンが
${ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }$
で表されるので運動方程式は
${ \displaystyle d x / dt=p_x / m \\ d p_x / dt =-x +ky \\ d y / dt =p_y /m \\ d p_y / dt = -y +kx }$

これは線形なので非線形性がないためカオスは現れないのじぇ。
f:id:daruma3940:20160520223745p:plain
そしてk=0の時トーラスっぽいものが現れていないのは
これは単純な調和振動子なので一度ポアンカレマップに乗った後運動をして、もう一度ポアンカレマップに乗ったときに完全に同じ点に乗ってしまう、
つまりトーラス上の一部しか運動をしないためトーラスが現れていないのじぇ

それに変数変換をすれば、2つの2次元調和振動子に分離もできるのじぇ
${ \displaystyle f(x)=(x^2+y^2)/2-kxy \\ \\ {\bf x}=\left( \begin{array}{c} x \\ y \end{array} \right) \\ \\ A = \left( \begin{array}{ccc} 1/2 & -k/2 \\ -k/2 & 1/2 \end{array} \right) \\ とすると \\ 固有ベクトルから \\ P= 1/\sqrt{2} \left( \begin{array}{ccc} -1 & 1 \\ 1 & 1 \end{array} \right) \\ \\ f(x)=　^t{\bf xAx} \\ \\ ^t{\bf xAx}={\bf (^txP) P^{-1}AP (P^{-1}x)\\=^t(^tPx)P^{-1}AP (P^{-1}x)\\=^t(^tPx)P^{-1}AP (^tPx)\\=^tx^{'}A^{'}x^{'} } \\ \\ \\ P^{-1}=^tP= 1/\sqrt{2} \left( \begin{array}{ccc} -1 & 1 \\ 1 & 1 \end{array} \right) \\ \\ A^{'}=P^{-1}AP=\left( \begin{array}{ccc} (1+k)/2 & 0 \\ 0 & (1-k)/2 \end{array} \right) \\ \\ {\bf x^{'} = ^tPx}=1/\sqrt{2} \left( \begin{array}{c} -x+y \\ x+y \end{array} \right) \\ 運動量は\\ P_{x'}=1/ \sqrt{2}(-P_x+P_y)\\ P_{y'}=1/ \sqrt{2}(P_x+P_y)\\ }$

A'は体格化されているのでx',y'のように変数変換をすれば2つの調和振動子に分けることができるのじぇ。
つまりこれはｋの値がなんであれトーラスでカオス性は持たないのじぇ

でもｋが0.6の時にはトーラスが出てきてないよね？？？これはなんで？？？
そしてトーラスの中心が2つに分かれているのはなんでなんだじぇ？？？
~~~追記~~~
f:id:daruma3940:20160520223745p:plain
k=0.6のときトーラスが現れていないのは新しい座標では振動数がそれぞれsqrt(1+k), sqrt(1-k) になっているのでk=0.6のとき周期の比が２になるので
片方が1周する間にもう片方がちょうど2周するので同じ点に帰ってきてしまい、トーラスが見えにくくなっているのじぇ

トーラスの中心は片方の振幅がゼロになる箇所に対応するのでどの方向の振幅がゼロになるかによって2種類あるので中心は2つあるのじぇ