daruma3940の日記

理解や文章に間違い等あればどんなことでもご指摘お願いします

カオスについて２

カオス

daruma3940.hatenablog.com
f:id:daruma3940:20160520223745p:plain
院試も終わったし前回の続きをかくのじぇ
前回2次元調和振動子は摂動を加えられなければトーラスになり、
摂動が弱い場合でも元のトーラスは変形して新しいトーラスができ、摂動が強くなるとトーラスが壊れてカオスが発生するらしいことについて書いたのじぇ。

f:id:daruma3940:20160520223745p:plain
ここでポアンカレマップについて説明するのじぇ。
ポアンカレマップとはトーラスの断面を切り取ったものなのじぇ。
f:id:daruma3940:20170824112349p:plain

2次元調和振動子の場合は変数はx,y,px,pyの4つであるけれど、
ハミルトニアンが一定という条件
{ \displaystyle H_0 = \sum_{i=1,2} (p_i^2+\omega_i^2q_i^2)/2 }
から変数（例えばpy）を一つ消せ、
y=0の点となった時に点をプロットするということをすれば
変数はx,pxだけになるので2次元平面に点をプロットできるようになるというわけのじぇ。
↓こんな感じ
f:id:daruma3940:20170824114046p:plain
f:id:daruma3940:20160520223745p:plain
ここで非加積分系について考えようじぇ。
{ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }

f:id:daruma3940:20170824142059p:plain
周期軌道から少しずらしたものがポアンカレマップのどこに来るのかを考えると

{ \displaystyle \delta x(T)=M \delta x(0) }

となるのじぇ。
このMは安定性行列と呼ばれ、保存系ではdet(M)=1となるのらしいのじぇ（よくわかってない）
これはリウビルの定理と呼ばれるものなのじぇ（リウビルの定理って正準変換のところで出てきたけど...）
{ \displaystyle M = \left( \begin{array}{ccc} a & b \\ c & d \end{array} \right) }
とすると
{ \displaystyle M \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} a \\ c \end{array} \right) }
{ \displaystyle M \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} b \\ d \end{array} \right) }
となり、
f:id:daruma3940:20170824143433p:plain
　　　　　　　　　　　　↓
f:id:daruma3940:20170824143442p:plain

面積S=ab-bc=det(M)=1
になるのでdet(M)は面積が何倍されたかを表すのじぇ。
ここで行列Mの固有値について考えると
{ \displaystyle det(M)=\lambda_1 * \lambda_2=1 \\ \lambda_1 = 1/\lambda_2 }

ここでもし固有値が実数で重解ではない場合、どちらか片方は固有値が1より大きく片方が固有値が1より小さくなるのじぇ
ということは片方は写像を繰り返すたびに指数関数的な拡大をし、
片方は写像を繰り返すたびに指数関数的に小さくなっていくのじぇ。
f:id:daruma3940:20170824163326p:plain
f:id:daruma3940:20170824163339p:plain
安定方向の直線上にない、つまり安定成分と不安定成分を持っているものは不安定性の指数関数的増加に引っ張られて不安定方向に流されていくのじぇ
f:id:daruma3940:20170824164353p:plain
もし固有値が複素数の場合、
λ1はλ２の複素共役かつλ1*λ２=|λ1|^2=1なので
{ \displaystyle \lambda_1 =exp(i \theta) \\ \lambda_2 =exp(-i \theta) }
になりこのような行列Mは
{ \displaystyle M = \left( \begin{array}{ccc} cosθ & sinθ \\ -sinθ & cosθ \end{array} \right) }
であり、これは回転行列なのじぇ。
これは指数関数的に拡大しないため安定なのじぇ。
f:id:daruma3940:20170824191827p:plain
もし重解を持った場合、
λ1=λ2=1であり、このような固有値を持つ行列は
{ \displaystyle M = \left( \begin{array}{ccc} 1 & a \\ 0 & 1 \end{array} \right) }
であり
{ \displaystyle M \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) }
{ \displaystyle M \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} a \\ 1 \end{array} \right) }

となるのじぇ。
図に書くとこんな感じ。
f:id:daruma3940:20170824191749p:plain

これも指数関数的に大きくなっていくわけではないので安定（中立安定）なのじぇ（この図あんまり理解できていない）
f:id:daruma3940:20170824191805p:plain


もし上のハミルトニアンでk=0のときこれは加積分系であり、周期軌道から少し初期値をずらしても別の周期軌道に乗るだけなのでこれは指数関数的に大きくなっていかず、中立安定的なのじぇ
しかしkが大きくなっていくとトーラスが壊れ、もしそれが複素数のほうへ壊れたのなら、安定固定点が発生し、実数のほうへ壊れたのなら不安定固定点が発生するのじぇ

このようすをkicked rotatormodelで描いてみるとこんな感じになったのじぇ
kicked rotatormodelとは
周期的に撃力を受ける回転子のことで....って書くのはめんどくさいので
http://a-phys.eng.osaka-cu.ac.jp/suri-g/phys8.html
このページを見てくれだじぇ
f:id:daruma3940:20170824160407p:plain

これがK（キックの強さ）=0の時
キックのじゃまを受けないのでひたすらθは大きくなっていくのじぇ
f:id:daruma3940:20170824160307p:plain
こんな感じ　まさしく中立安定
K=0.01のとき
f:id:daruma3940:20170824160435p:plain
K=1.2の時
f:id:daruma3940:20170824160514p:plain
島みたいなのが現れているのじぇ。これが複素数の方向に壊れたやつなのじぇ。
島と島の間には実数の方向に壊れたやつが存在しているけどカオス的になってしまっているので構造はみてとれないのじぇ
ちなみにこの島を拡大すると島の中にも島が存在するのじぇ。これはいわゆるフラクタル的構造なのじぇ
f:id:daruma3940:20170824160921p:plain
さらにキックを強くするとこんな感じ
f:id:daruma3940:20170824160713p:plain


これらの図は範囲が違ったりするので注意なのじぇ
Kが大きくなると完全にカオス的になるのはすべて実数方向にずれるから？？
安定固定点と不安定固定点が交互に出てくるのはなぜ？？？
さっきの
{ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }

についてもやってみたけどそんなにきれいなのは見られなかったのじぇ
でもまあ一応張っておくか
f:id:daruma3940:20170824183931p:plain
f:id:daruma3940:20170824172501p:plain
f:id:daruma3940:20170824195423p:plain
f:id:daruma3940:20170824223802p:plain
f:id:daruma3940:20170824223818p:plain
f:id:daruma3940:20170825113033p:plain
f:id:daruma3940:20170824223831p:plain
f:id:daruma3940:20170826195420p:plain
f:id:daruma3940:20170826184006p:plain

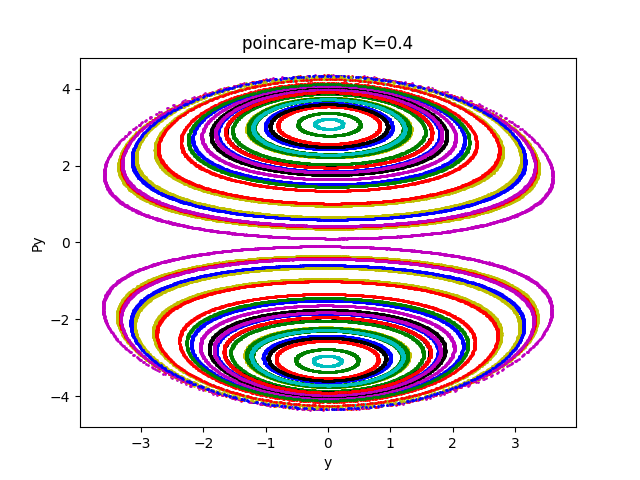
なんかうまくいかないなーー
なんでだろうだじぇ？


う～～んう～～ん......
f:id:daruma3940:20160520223745p:plain
分かったのじぇ
ハミルトニアンが
{ \displaystyle H_0 = (p_x^2+p_y^2+x^2+y^2)/2 -kxy }
で表されるので運動方程式は
{ \displaystyle d x / dt=p_x / m \\ d p_x / dt =-x +ky \\ d y / dt =p_y /m \\ d p_y / dt = -y +kx }

これは線形なので非線形性がないためカオスは現れないのじぇ。
f:id:daruma3940:20160520223745p:plain
そしてk=0の時トーラスっぽいものが現れていないのは
これは単純な調和振動子なので一度ポアンカレマップに乗った後運動をして、もう一度ポアンカレマップに乗ったときに完全に同じ点に乗ってしまう、
つまりトーラス上の一部しか運動をしないためトーラスが現れていないのじぇ

それに変数変換をすれば、2つの2次元調和振動子に分離もできるのじぇ
{ \displaystyle f(x)=(x^2+y^2)/2-kxy \\ \\ {\bf x}=\left( \begin{array}{c} x \\ y \end{array} \right) \\ \\ A = \left( \begin{array}{ccc} 1/2 & -k/2 \\ -k/2 & 1/2 \end{array} \right) \\ とすると \\ 固有ベクトルから \\ P= 1/\sqrt{2} \left( \begin{array}{ccc} -1 & 1 \\ 1 & 1 \end{array} \right) \\ \\ f(x)=　^t{\bf xAx} \\ \\ ^t{\bf xAx}={\bf (^txP) P^{-1}AP (P^{-1}x)\\=^t(^tPx)P^{-1}AP (P^{-1}x)\\=^t(^tPx)P^{-1}AP (^tPx)\\=^tx^{'}A^{'}x^{'} } \\ \\ \\ P^{-1}=^tP= 1/\sqrt{2} \left( \begin{array}{ccc} -1 & 1 \\ 1 & 1 \end{array} \right) \\ \\ A^{'}=P^{-1}AP=\left( \begin{array}{ccc} (1+k)/2 & 0 \\ 0 & (1-k)/2 \end{array} \right) \\ \\ {\bf x^{'} = ^tPx}=1/\sqrt{2} \left( \begin{array}{c} -x+y \\ x+y \end{array} \right) \\ 運動量は\\ P_{x'}=1/ \sqrt{2}(-P_x+P_y)\\ P_{y'}=1/ \sqrt{2}(P_x+P_y)\\ }

A'は体格化されているのでx',y'のように変数変換をすれば2つの調和振動子に分けることができるのじぇ。
つまりこれはｋの値がなんであれトーラスでカオス性は持たないのじぇ

でもｋが0.6の時にはトーラスが出てきてないよね？？？これはなんで？？？
そしてトーラスの中心が2つに分かれているのはなんでなんだじぇ？？？
~~~追記~~~
f:id:daruma3940:20160520223745p:plain
k=0.6のときトーラスが現れていないのは新しい座標では振動数がそれぞれsqrt(1+k), sqrt(1-k) になっているのでk=0.6のとき周期の比が２になるので
片方が1周する間にもう片方がちょうど2周するので同じ点に帰ってきてしまい、トーラスが見えにくくなっているのじぇ

トーラスの中心は片方の振幅がゼロになる箇所に対応するのでどの方向の振幅がゼロになるかによって2種類あるので中心は2つあるのじぇ

息抜き

f:id:daruma3940:20160520223745p:plain
院試の勉強つまらんので息抜きに将棋盤アプリ作り始めてみたら
息抜きのほうに力が入ってしまっていたのじぇ......

f:id:daruma3940:20170816224032p:plain

f:id:daruma3940:20160521003616p:plain
何やってんのよ....
f:id:daruma3940:20160520223745p:plain
なにやってんだろうなぁ~~~~~~~~~~~~~~~~
f:id:daruma3940:20160520223745p:plain
うちの教授陣は優しいのできっと....きっと私の解けなかった問題の配点を0点にしてくれるはずなのじぇ.....
f:id:daruma3940:20160709192554j:plain
....(;^_^A

Rotated Bitboardなのじぇ

コンピューター将棋 アルゴリズム


Rotated Bitboardについての解説をしようじぇ？

Bitboardについての解説は以前の記事を見てくれだじぇ。
daruma3940.hatenablog.com




SquirrelはRotated Bitboardを使って効きのある升を計算しているよ！


最近はPEXTbitboardとかもあるらしいじゃない？どうしてRotated Bitboardを使うの？

https://twitter.com/search?q=Rotated%20from%3Amerom686&src=typdtwitter.com
mermoさん曰くPEXTよりも早いそうなのじぇ。
そしてまりちゃのPCはアルバイトして買った学習用i7-4770K以外のPCはAVX2に対応していなくてPEXTは使えないのでRotatedにせざるを得なかったのじぇ。


Bitboardによる効きの表現は効きのあるマスに対応するbitを1にすることである駒がどこに効きを作っているのかを表現するというものなのじぇ。
しかし長い効きを持つ駒の場合効きを遮る駒がどこにあるのかによってどこまで効きを伸ばすことができるかが変わってくるのじぇ。
そこで、（とびゴマの位置、邪魔ゴマの位置）全通りに対してどこに効きを発生させることができるかのTable集を作成し、どこに邪魔ゴマがあるかをindexにしてそのテーブルを引っ張ってくることで効きを表現しようという方法なのじぇ。


例えば
青いマスを邪魔ゴマがいるマス、赤いマスを効きを発生させている駒の升だとすると

この図で4の場所にいる飛車の縦方向のききを求めたければ
TateKikiTable[4(効きを発生させる駒の場所)][(bitboard>>1)&(7)] のようになるのじぇ
今のbitboardをシフトして必要なところだけマスクして取り出すことによって　Tableのindexを作成できるのじぇ


この場合は
TateKikiTable[31(効きを発生させる駒の場所)][(bitboard>>28)&(7)]になるのじぇ


しかし横の効きを求めるためにはこのマスの番号のつけ方では

シフトとマスクではindexを作れないのじぇ。

そこでこのbitboardを90度回転させたboard(bitboard90とする)を作成すれば

これはさっきと同じようにシフトとマスクでindex作成できるのじぇ。


実際のbitboardは64bit整数２つ（ここではint64_t bb[2]とする）で作られるためbb[0]かbb[1]かどちらを参照するべきかも指定しないといけないためもうちっとふくざつになるのじぇ
斜め＋４５度斜め-４５度についても似たような感じなのじぇ。

もし将棋の駒がすべて近接駒ならRotated Bitboardなんて技術は必要ないのじぇ。
Rotated Bitboardは長い効きを持つ駒の効きを考慮するために必要なのじぇ

ちなみにこれがSquirrelにおけるRotated Bitboardの設計図なのじぇ



あと駒のいる位置を表しているbitboard(occupied bitboad)は
回転無し,90度回転+45度回転,-45度回転の４つ保持しないといけないのだけれど

縦方向の効きは1段目9段目に邪魔ゴマがあっても1段目9段目に効きを作ることができるので縦方向occupiedbitboardは1段目9段目を表すbitを除いて7*9=63bitあればよく
横方向も1筋目9筋目のbitはいらないので7*9=63bit
斜めはそれぞれ7*7=49bitあればよいので
実はoccupiedbitboardはすべて256bitに収めることができ
これによって駒が動いた時のoccupiedbitboardのこうしんの処理はSIMD演算を使えば一気に処理できるのじぇ。
これを用いれば結構高速化できた記憶があるのじぇ

open ai gym[atari]をwindowsでも使えるようにしようじぇ？？

f:id:daruma3940:20160520223745p:plain
なんかopen ai gym[atari]をwindows環境で

 pip install gym[atari]

しようとしたらインストールできなかったので
ビルドする方法をいろいろ調べてやってみたのでここに書き記しておきのじぇ
ちなみにbash on windowsとか vcXsrv とか使うのはめんどくさいのでそれを使わない方法なのじぇ（MSYS2は使ってる）
f:id:daruma3940:20160520223745p:plain
まあこのQuitaの方法のそのまんまなのでこれ読めばわかるって人はこれ読んでくれだじぇ
qiita.com

f:id:daruma3940:20160520223745p:plain
github.com
このissueの
f:id:daruma3940:20170813025408p:plain
この投稿に注目なのじぇ

github.com
どうやらこれをつかえばいいらしいのじぇ？

pip install -U git+https://github.com/Kojoley/atari-py.git

f:id:daruma3940:20160520223745p:plain
まりちゃのPCにはすでにMSYS2環境はすでにあってそこにpathも通っていたので
Visualstudio 2015のC++ビルドツールさえ用意すれば　うまくいったのじぇ

f:id:daruma3940:20170813025746p:plain
(このソースは
github.comより

)
f:id:daruma3940:20160520223745p:plain
うむ！ちゃんと動いてるみたいなのじぇ！



f:id:daruma3940:20170813025834p:plain

f:id:daruma3940:20160520223745p:plain

早く公式で対応して..(懇願)

open ai gym[atari]をwindowsでも使えるようにしようじぇ？？

f:id:daruma3940:20160520223745p:plain
なんかopen ai gym[atari]をwindows環境で

 pip install gym[atari]

しようとしたらインストールできなかったので
ビルドする方法をいろいろ調べてやってみたのでここに書き記しておきのじぇ
ちなみにbash on windowsとか vcXsrv とか使うのはめんどくさいのでそれを使わない方法なのじぇ（MSYS2は使ってる）
f:id:daruma3940:20160520223745p:plain
まあこのQuitaの方法のそのまんまなのでこれ読めばわかるって人はこれ読んでくれだじぇ
qiita.com

f:id:daruma3940:20160520223745p:plain
github.com
このissueの
f:id:daruma3940:20170813025408p:plain
この投稿に注目なのじぇ

github.com
どうやらこれをつかえばいいらしいのじぇ？

pip install -U git+https://github.com/Kojoley/atari-py.git

f:id:daruma3940:20160520223745p:plain
まりちゃのPCにはすでにMSYS2環境はすでにあってそこにpathも通っていたので
Visualstudio 2015のC++ビルドツールさえ用意すれば　うまくいったのじぇ

f:id:daruma3940:20170813025746p:plain
(このソースは
github.comより

)
f:id:daruma3940:20160520223745p:plain
うむ！ちゃんと動いてるみたいなのじぇ！



f:id:daruma3940:20170813025834p:plain

f:id:daruma3940:20160520223745p:plain

早く公式で対応して..(懇願)

カオスについて

カオス

f:id:daruma3940:20160520223745p:plain
暇なのでカオスについてかたろうじぇ？
f:id:daruma3940:20160521003616p:plain
いきなりね

f:id:daruma3940:20160520223745p:plain
カオスの定義はいろいろあるけれどたぶん「初期値俊敏性を持っていて決定論的であるもののこと」なのじぇ
f:id:daruma3940:20170803230209p:plain

この図でいう
{ \displaystyle \lambda > 0 }
を持つものなのじぇ



f:id:daruma3940:20160520223745p:plain
昔流れてきたこのツイートも大まかに言ってカオスなのじぇ。

f:id:daruma3940:20160521003616p:plain
はぇ～～～

f:id:daruma3940:20160520223745p:plain
2次元調和振動子の場合を考えてみようじぇ。
これがハミルトニアンなのじぇ
{ \displaystyle H_0 = \sum_{i=1,2} (p_i^2+\omega_i^2q_i^2)/2 }

f:id:daruma3940:20160520223745p:plain

f:id:daruma3940:20160520223745p:plain
見ての通りこの場合ハミルトニアンはx方向のものとy方向のものに分離できるのじぇ。
{ \displaystyle H_0 = \sum_{i=1,2} (p_i^2+\omega_i^2q_i^2)/2　≡ H_{0x}+H_{0y} }
そしてこれら
{ \displaystyle H_{0x} 　と　H_{0y}　は保存されるのじぇ。 }
{ \displaystyle \{H_x,H\}_{classical} =dH_x/dt=0　 ---(1) }

f:id:daruma3940:20160520223745p:plain
xについて見てみるとこれは位相空間的に周期的なのじぇ。

f:id:daruma3940:20170804214947p:plain

そしてもちろんyについても周期的なのじぇ。
xについても周期的そしてyについても周期的ということはこれは位相空間上でトーラスになるのじぇ。

f:id:daruma3940:20170804215634p:plain

f:id:daruma3940:20160520223745p:plain

ここでさっきの方法をちょっとだけ変えてトーラスであることを示すのじぇ。
（１）のハミルトニアンの力学変数を作用変数
{ \displaystyle J_i=(2\pi)^{-1} \oint p_i dq_i }
と角変数
{ \displaystyle \phi_i = \omega_i t }
に正準変換してみようじぇ。
まあ難しいことしなくてもここでは調和振動子なので作用変数は
縦軸
{ \displaystyle \sqrt{2E} }
横軸
{ \displaystyle \sqrt{2E}/\omega }
の楕円になるので
f:id:daruma3940:20170805124806p:plain

楕円の面積の公式
{ \displaystyle S=\pi ab }
を用いれば
{ \displaystyle S=2 \pi E / \omega \\ より \\ J=E/ \omega }
このように計算でき、ハミルトニアンは
{ \displaystyle H_0 = \sum_{i=1,2} \omega_i J_i　≡ H_0(J_1,J_2) }
このように書き直せるのじぇ。
ここで
{ \displaystyle dJ_i/dt=-\partial H_0 /\partial \phi_i =0 }

であるので{Ji}は保存されるのじぇ。
これによってさっきの話と同じようにトーラスになることが分かったのじぇ。



f:id:daruma3940:20160520223745p:plain
今度はこれに非加積分摂動を与えた場合を考えようじぇ。
{ \displaystyle H_0 = H_0(J_1,J_2) + \epsilon \sum_{m,n} f_{m,n}(J_1,J_2)cos(m \phi_1 + n \phi_2) ---(2) }
非加積分摂動はフーリエ展開の形で与えるのじぇ。

ここで母関数を
{ \displaystyle W= J'_1 \phi_1 + J'_2 \phi_2 +\epsilon \sum_{m,n} g_{m,n}(J'_1,J'_2)cos(m \phi_1 + n \phi_2) }

として　新しい作用、各変数
{ \displaystyle \{ J'_i , \phi '_i \} }
を導入した正準変換を考えると
{ \displaystyle J_i= \partial W/\partial \phi_i= J'_1 +\epsilon \sum_{m,n} (m\delta_{i 1}+n\delta_{i 2}) g_{m,n}(J'_1,J'_2)cos(m \phi_1 + n \phi_2) }

なので(2)をJ'iの周辺でテーラー展開したものは,
{ \displaystyle H = H_0(J'_1,J'_2) + \sum_{i=1,2} ( \partial H_0/\partial J_i ) ( J_i -J'_i )+ ... \\ = H_0(J'_1,J'_2) + \epsilon \sum_{m,n} [ f_{m,n}+ (m\omega_1+n\omega_2)g_{m,n} ] cos(m \phi_1 + n \phi_2) +O(\epsilon^2) }

になるのじぇ。

。もし摂動が小さく任意のm,nに対して
{ \displaystyle | f_{m,n} | << | m\omega_1+n\omega_2 | }
が成立するのであれば、
{ \displaystyle g_{m,n}=-f_{m,n}/(m\omega_1+n\omega_2) (<<1) }
のようにgを選ぶことでテーラー展開のεの一次の項を消すことができるのじぇ。
もし
{ \displaystyle \gamma=\omega_1/\omega_2 }
が有理数の場合は分母を発散させるm,nの選び方ができてしまうのでg関数は決まらないけれど、
有理数の数は無理数の数に比べてとても少ないのでそれは無視できると考えられるらしいのじぇ。

この手続きをεの高次の項に対しても繰り返すことで高次の項を消去でき、
ハミルトニアンは結局
{ \displaystyle H=H_0(J^{(∞)}_1,J^{(∞)}_2) }


となり、元のトーラスは変形して新しいトーラスができるのじぇ。
これを Kolmogorov-Arnold-Moser(KAM) トーラスというらしいのじぇ。
f:id:daruma3940:20160520223745p:plain
gをどう選ぶかの話のにいろいろ疑問を持つ人は多いと思うけれどそこはかなり難しい数学の議論でKolmogorov-Arnold-Moserの論文に詳しく書かれているらしいのじぇ。



。もし摂動が大きくなってくると、
{ \displaystyle | f_{m,n} | >> | m\omega_1+n\omega_2 | }
となり、
{ \displaystyle | g_{m,n} |<< 1 }
となる母関数を得ることができず、εの一時の項を消せないためトーラスは崩壊するのじぇ。これがカオスの発生なのじぇ。


ところでなぜ母関数が
{ \displaystyle | g_{m,n} | << 1 }
を満足しなければならないのかはまりちゃにはわからないのじぇ（詳しい人いたら教えてください。）


f:id:daruma3940:20160520223745p:plain
本の内容をブログに書いてみればよくわかるんじゃないかと思ったけれど
大事で気になるところがはしょられているのでいまいちよくわからんって感じなのじぇ
f:id:daruma3940:20160520223745p:plain
トーラスが崩壊してカオスがどのように作り出されるか
ポアンカレマップ、面積保存写像、孤立固定点についてkicked rotator modelの図を交えた話はまた今度気が向いたらなのじぇ


～～～～追記～～～～
f:id:daruma3940:20160520223745p:plain
KAMトーラスなんて現実世界に現れるのかと思うかもしれないけど
うちの教授によるとなんと土星の環がKAMトーラスらしいのじぇ
土星の太陽を回る周期と,土星の輪をなしている塵が土星の周りを回る周期でトーラスを形成しほかの惑星によって及ぼされる引力が微小な摂動となり
周期比が有理数比から遠いところだけが輪として残っているということらしいのじぇ
f:id:daruma3940:20171116212310j:plain
写真はここから
solarsystem.nasa.gov

■

f:id:daruma3940:20160521003616p:plain

ちょっとまりちゃ。最近全然将棋プログラム書いてないじゃない！

次の電王トーナメントのために何かしなさいよ！

f:id:daruma3940:20160520223745p:plain

一応電王トーナメントに関係することはしているのじぇ。

f:id:daruma3940:20160521003616p:plain

え？何してるの？

f:id:daruma3940:20160520223745p:plain

ゲーム作ってるのじぇ。

f:id:daruma3940:20160521003043p:plain

は？

f:id:daruma3940:20170716150153p:plain

 

f:id:daruma3940:20160520223745p:plain

Tower of DenOuなのじぇ。

f:id:daruma3940:20160521003616p:plain

えぇ....

f:id:daruma3940:20160520223745p:plain

せかいの　まんなかにたつ　とうは

でんおうに　つうじている　という


はるかな　でんおうを　ゆめみて
おおくの　ものたちが
このとうの　ひみつに　いどんでいった　
だが　かれらの　うんめいを
しるものはない

そして　いま　またひとり‥‥

f:id:daruma3940:20160521003616p:plain

魔界塔士かよ！

 

f:id:daruma3940:20170716150538p:plain

f:id:daruma3940:20160520223745p:plain

あの鳥はcoduck,あのうさぎはlesserpyonなのじぇ

ゲームとしてはロックマン的な感じにしたいのじぇ。

f:id:daruma3940:20170716150900p:plain

f:id:daruma3940:20160520223745p:plain

これが最初のボスうさぴょんなのじぇ。

ジャンプしながら攻撃を仕掛けてくるのじぇ

 

f:id:daruma3940:20170716151018p:plain

f:id:daruma3940:20160520223745p:plain

これはBonanza。3駒連携攻撃をしてくるのじぇ。

 

f:id:daruma3940:20170716151143p:plain

f:id:daruma3940:20160520223745p:plain

これは技巧。

いまいち仕様が決まってないのじぇ。

f:id:daruma3940:20170716151340p:plain

f:id:daruma3940:20170716151436p:plain

f:id:daruma3940:20170716151636p:plain

f:id:daruma3940:20160520223745p:plain

ゲーム開発は楽しいのじぇ。

 

f:id:daruma3940:20160520223745p:plain

ちなみにちょっと遊べるぐらいのクオリティになってきたので友達にテストプレイとして公開してみたけどだれも遊んでくれなかったのじぇ
この「遊んでくれてありがとう」画面を作った意味がなくなってしまったのじぇ

f:id:daruma3940:20170716151942p:plain

f:id:daruma3940:20160521003616p:plain

ざんねんね。

f:id:daruma3940:20160520223745p:plain

今の課題としては難易度調整がダメダメで技巧よりもうさぴょんのほうが強くなってしまっていること、ボリュームが足りていないこと、音楽を自作しようとしているが全然作曲ができていないことなのじぇ。

 あとこういうサガフロみたいな感じのゲームつくるのも面白そうだじぇ